スポンサーリンク
はじめに
前回の記事で、Excelの財務関数について導入の話をした。
FP(ファイナンシャル・プランナー)試験で扱われる有名な係数が6つあるのだが、今回はそのうち
- 終価係数
- 年金終価係数
- 減債基金係数
という3つの係数を、財務関数と関連付けて説明する。
なおこれら「係数」っていうのは本来、1円当たりに対するパーセンテージとかを指すものだが、元手5,000円だったとして<5,000円×係数>で求められる結果のこととかも「係数」と混同して表記することにする。
サンプルデータはこちらのファイル。
終価係数→FV関数
例題その1―終価係数
ではまず、終価係数という係数についての例題。
このくらいなら、複利という言葉の例としてよく挙げられるものであり、割とすんなり解けるのではないだろうか。
各年の年末には、年初の金額に対し2%の率で利息が加わるから、
1年目の末の金額A1は、 A1=100万×(1+2%)
2年目の末の金額A2は、 A2=A1×(1+2%)=100万×(1+2%)2
3年目の末の金額A3は、 A3=A2×(1+2%)=100万×(1+2%)3
・・・と続いていくのが複利というものであり、
10年目の末の金額A10は、A10=100万×(1+2%)10 で、これが求める答えになる。
もちろん(1+2%)10なんて計算を、電卓でやるものではない。
次のようにExcelでやれば良く、例題の答えは1,218,994円ということだ。
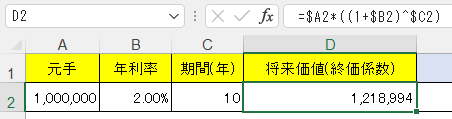
つまり一般化すると、元手a、利率r、期間nとして複利で運用したときの将来価値というやつは、終価係数というもので求めるけど、その式は
終価係数FV=a(1+r)n
となる。
そしてこれをFV関数で求めると、次のようになる。まあこのくらいの問題なら本当に、FV関数を使う必要もそうないだろう。
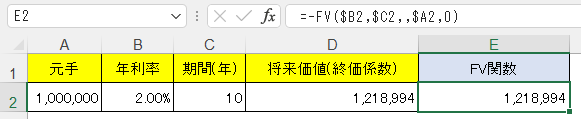
年金終価係数→FV関数
例題その2―年金終価係数
→答え:183,994円
利率を年単位で与えておきながら、月単位の積立ということにされていて、ややこしくなっている。
他にも先程の<例題1>では積立というものはなく、最初に100万円を入れたらそれっきり、利息が付くのに任せるという形だった。
ではここから、やり方をじっくり見ていこう。
まず年利率が1.5%とあるけど、1ヶ月ごとの支払だったら、12で割った、<1.5%÷12>の利率が毎月適用になる。この辺がまた、慣れてないと分かりにくいところだけどね。
この<1.5%÷12>を毎回書くのは面倒だから、r = 1.5%÷12としよう。
月末に積み立てるってことなので、1ヶ月目に積み立てた5,000円という金額は、翌月末=2ヶ月目の末日には利息が付いて
5,000+5,000×( 1.5%÷12 ) = 5,000×( 1+1.5%÷12 )=5,000×( 1+r )
という金額に化ける。
じゃあ3ヶ月目・月末の金額は、今のに同様に毎月の利率を乗じて
5,000×( 1 + r )2
となる。
これをずっと続けていくと、利息適用後、36ヶ月目の残額は 5,000×(1+r)35円となる。
1ヶ月目の月末に入れてた5,000円は36ヶ月目には 5,000×(1+r)35 となるらしい。
じゃあ1ヶ月遅れて、2ヶ月目の月末に入れてた5,000円は、36ヶ月目には 5,000×(1+r)34 円になるだろう。
この調子で行けば、36ヶ月目には、毎月入れてる5,000円はそれぞれ次の金額に化けていることになる。
| 1ヶ月目の月末に入れてた5,000円 | 5,000×(1+r)35 |
| 2ヶ月目の月末に入れてた5,000円 | 5,000×(1+r)34 |
| ・・・ | |
| 36ヶ月目の月末に入れてた5,000円 | 5,000×(1+r)0 |
ちょっとした数学
ここからはちょっとした数学の話になる。
数学に馴染みない人にも(私も偉そうに言えるレベルじゃないが)なるべく分かるようにしていくけど、まず次の公式だけは押さえておきたい。
簡単証明:左辺=S とすると、S-x・S = 1-xn+1だから、
S= (1-xn+1 ) / (1-x) = (xn+1 – 1) / (x-1)
年金終価係数の公式を導出
さて、毎月入れてる5,000円はそれぞれ、次の金額に化けているのだった。
| 1ヶ月目の月末に入れてた5,000円 | 5,000×(1+r)35 |
| 2ヶ月目の月末に入れてた5,000円 | 5,000×(1+r)34 |
| ・・・ | |
| 36ヶ月目の月末に入れてた5,000円 | 5,000×(1+r)0 |
もうこの際、更に面倒だからR=1+rとしよう。すると上記の総合計は、前述の公式も合わせて
5,000 × (R0+R1+・・・・・・R35 )
= 5,000 × (1+R1+・・・・・・R35 )
= 5,000 × (R35+1-1 ) / (R-1)
= 5,000 × {( 1 + r )36-1 } / {( 1 + r )-1}
=5,000 × {( 1 + r )36-1 } / r
rというのが元々、年利率を12で割ったものだったから、この式をExcel上で表現したのが次のようになる。

そしてFV関数で同一の結果を求めたものがこちら。

また一般化すると、元手t、期間n、利率rの複利で運用したときの将来価値(→年金終価係数による将来価値)を求める式が次のようになる。
年金終価係数による将来価値FV = t{( 1 + r )n – 1 } / r
減債基金係数→PMT関数
年金終価係数に関する例題その2を再掲。
→答え:183,994円
さて、この問題では毎月の積立額5,000円が与えられていて、そこから将来の累計積立金額183,994円を答えとして求めた。
では逆に、
- 毎月の積立額が不明→t円とする
- 累計積立金額183,994円を、年利率1.5%の条件下で将来の累計積立金額の目標値として(もちろん実際にはもっとキリの良い数値にするだろうが)設定する
という条件で、毎月の積立額t円(答え:5,000円)を求めたいということもあるだろう。
一般的な問題文としては、<年利1.5%で3年後に183,994円を貯めたい場合、毎月の積立額tを幾らにすれば良いか?>というように書かれるだろう。多分この問題文だけ、予備知識なしで見せられても、戸惑うばかりの人が多いのではないだろうか。
この積立額t円を求めるのが、減債基金係数だ。
じゃあもうこの減債基金係数ってやつは、年金終価係数の逆を取れば良いということなので、上記で求めた年金終価係数の公式
FV=t{(1+r)n-1 } / r
の分母・分子について逆を取ろう。上記で言う、将来の累計積立金額183,994円をSと置くと、減債基金係数の公式は
減債基金係数=rS / {(1+r)n-1 }
となる。この導出した公式を当てはめて計算したのが下図だ。

そして、この減債基金係数はPMT関数で求められる。
それで同一の結果を求めたものがこちら。

関数の構成
FV関数の構成
では改めて、上記で使った関数について、ケースごとに式をはっきり書いてみよう。
まずはFV関数の構成。
図の上では空欄となっている引数は、0を埋めても同じなので、0を埋めて表記してみる。
まず、最も簡単な終価係数をFV関数で求めたもの。
=-FV($B2, $C2 , 0, $A2, 0)

次に、積立がある年金終価係数をFV関数で求めたもの。
=-FV($A2/12,$B2*12 , $C2 , 0, 0)

FV関数の引数の構成を改めてまとめ直すと、次のようになるということだ。③定期支払額と④現在価値について、終価係数を求める場合と年金終価係数を求める場合とでひっくり返る。
| ①利率(必須) | 年利率が与えられているが月単位で計算する場合は、12で割る。 |
| ②期間(必須) | 返済や積立の期間。 年単位で期間が与えられているが月単位で計算する場合は、12を乗じる。 |
| ③定期支払額(必須) |
毎回支払う金額。 終価係数を求める場合は、空欄か0 (終価係数って、1回入金してそれきりだから、定期支払は無い) |
| ④現在価値 (省略可) |
頭金。 終価係数を求める場合は、元手の金額を書く |
| ⑤支払期日 (省略可) |
0(省略)→月末・期末の支払 今回の解説では、月末支払=0 を想定して進める。 |
PMT関数の構成
次に、減債基金係数を求めたPMT関数の構成。
=-PMT($A2/12,$B2*12,0,$D2,0)

引数の構成をまとめ直すと、下図のような感じ。
PMT関数は次回の記事でも出てくるから、そのときも再掲する。
| ①利率(必須) | 年利率が与えられているが月単位で計算する場合は、12で割る。 |
| ②期間(必須) | 返済や積立の期間。 年単位で期間が与えられているが月単位で計算する場合は、12を乗じる。 |
| ③現在価値(必須) |
将来価値が与えられてて、そこから毎回の積立額などを求める場合に記入 |
| ④将来価値 (省略可) |
現在価値が与えられてて、そこから毎回の積立額などを求める場合に記入 |
| ⑤支払期日 (省略可) |
0(省略)→月末・期末の支払 今回の解説では、月末支払=0 を想定して進める。 |
実際に積立予定表を作る
さて上記で、Excel関数の他に数学的な求め方もやってみたが、これでもまだ煙に巻いたような数式で求めているだけで、実感は湧きにくい。
FP試験とか、Excel財務関数とか言って勉強に取り組んでみたところで、1行で片付くような数式を眺めてたってそう理解できるものでもないだろう。多くの人が恐らくそれだけでとどまっているから、財務関数をただ使うだけで終わっているはずだ。
やはり面倒そうでも、自分で36ヶ月分の積立予定表をきちんと作って、1ヶ月ごとの数字を全部足し合わせてみた結果が合致するところまで確認するべきだろう。
まあFV関数くらいなら、積立予定表の作成はそう難しいことではない。
(毎月の積立額t)×(1+年利率r ÷ 12)月数
を36ヶ月分計算して、それを全部足し合わせれば良いだけだ。
下図のような式を36ヶ月分コピーすれば良い。
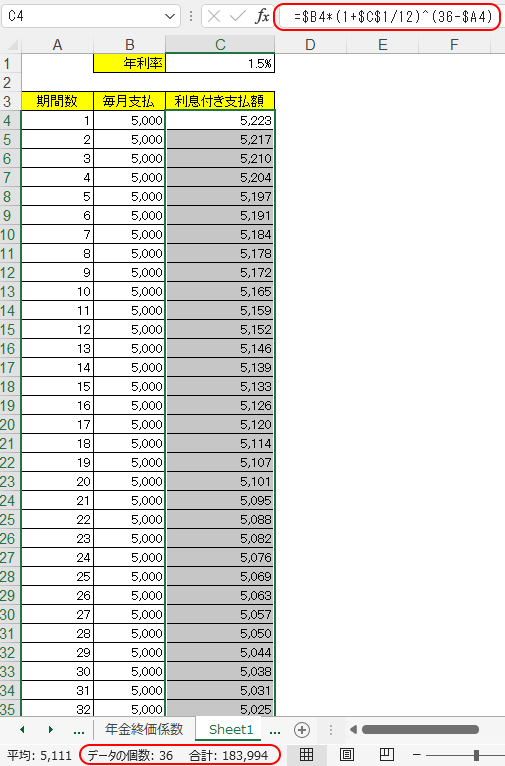
将来価値とか、用語の意義
ではそもそもの話に帰って、今回の問題とした将来価値とは何なのかだが、予備知識がなくてもだいたい分かったのではないだろうか。
年金終価係数の例を思い出そう。普通に5,000円が36ヶ月分では180,000円になるだけだが、年利率1.5%という利息まで含めて毎月積立をすれば累積183,994円に増えてくれるらしい。
そこまで加味した将来の累積金額を、最初で計算しようということだ。
各係数の内容について、私なりの言葉でまとめると次のようになる。
| 係数 | Excelの関数 | 内容 |
| 終価係数 | FV | 最初に1回こっきり入金したお金が、定期的に利息が付く複利のもとで、将来いくらに増えるか。 |
| 年金終価係数 | 終価係数とは違い、入金は1回こっきりではなく定期積立する条件で、それら各期の積立に利息が付く複利のもとで、将来いくらに増えるか。 | |
| 減債基金係数 | PMT | 年金終価係数の問題で、「将来累計いくらに増やしたい」という目標が先にあったときに、それに対応する毎期の積立金額はいくらにすれば良いか。 |
スポンサーリンク