スポンサーリンク
はじめに
Excel財務関数で、現在価値を求めるPV関数についての記事を以前に書いた。
今回はそのPV関数の派生・発展版というか、色々と不規則なパターンにも対応しながら、投資判断に使える現在価値を求められるバージョンの関数を紹介する。
PV関数のときは、ローン返済の事例を扱った。今回扱う関数もそれで行けなくはないが、<投資に対しどれだけのキャッシュフローを回収できるか>という用途に用いることが多いので、それで進めていく。
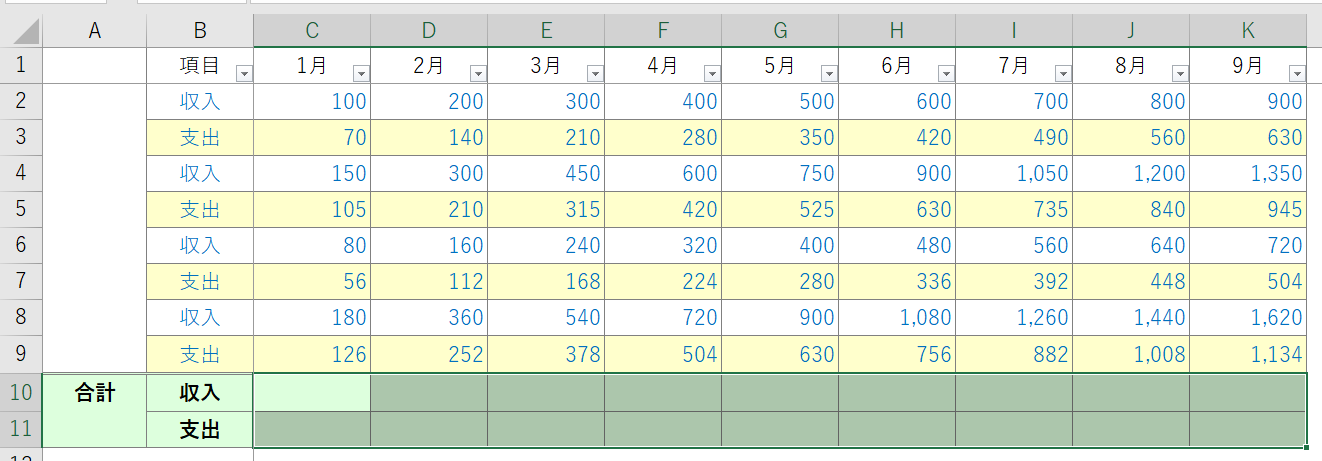
PV関数についての記事で、年金現価係数を求める際に使ったのが下図の表だ。またそのときのサンプルファイルはこちらになる。
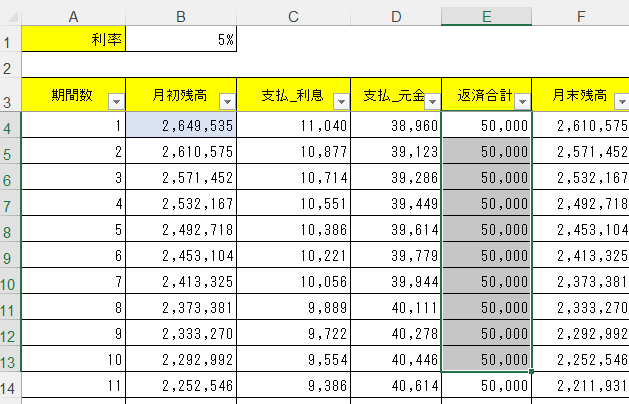
年金現価係数において扱った上図では、E列で毎回50,000円を返済するということになっている。
つまりこれは①一定の期間で、②一定の金額を、返済する規則性を前提にしたものだ。
NPV関数:返済期日は規則的、返済金額は不規則
では下図のような例を考えてみる。このサンプルファイルはこちら。
2行目・期間数=0の行は、初期投資についての行だが、いったんこれは考えずにいく。
PV関数のときの返済額(元金+利息)に該当するのが、F列のキャッシュフローだ。
そして今回のポイントは、その金額が不規則であることだ。ただし返済の期間は、1年ごとなど一定の規則に従う。
A列の利率(正確には、割引率という)も一定で不変なんだけど、これは後でちょっとした計算において変化させる。
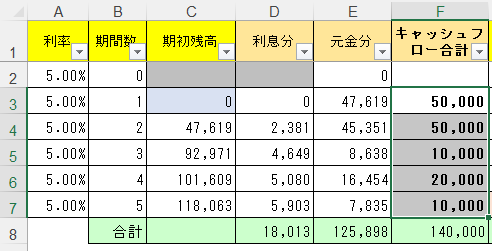
さて今回の問題だけど、F列のキャッシュフローってやつの合計140,000円について、割引率5%を考慮して割引いた現在価値というやつを求めたいということだ。
その最終的な答えは、E8セルに示した125,898円になる。これを考えていこう。
では今回求めたいE8セルの答えは、第1期~第5期それぞれの現在価値の累積となる。
その各期の現在価値というのは、第n期については< 第n期のキャッシュフロー÷(1+割引率)n >で求められる。
(この式の導出は、なんとなく感覚的に分かってもらえるかと思うので、詳細は省略)
その式を下図のように、E列に入れてみる。そしてその総合計が、E8セル(と、G7セル)に125,898円と求められ、これが結果的に最終的に求めたい答えとなる。
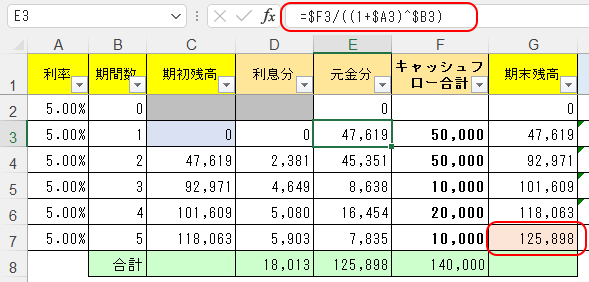
さてG列「期末残高」というのは、C列=期初残高に、E列を加えたものだ。
E列とは、<各月キャッシュフローを利息・元金に分けたうち元金分>とも言えるし、<各月キャッシュフローの現在価値の分>とも言える。
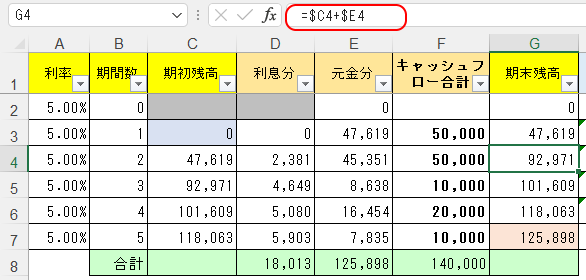
このG列と合致する答えが、NPV関数で求められる。H3セルに
=NPV( $A3 , $F$2:$F3 )
と入れて、後はそれをH7セルまでそのままコピーすれば良い。
起点のF2セルについて、F$2という複合参照にするのを忘れないように。
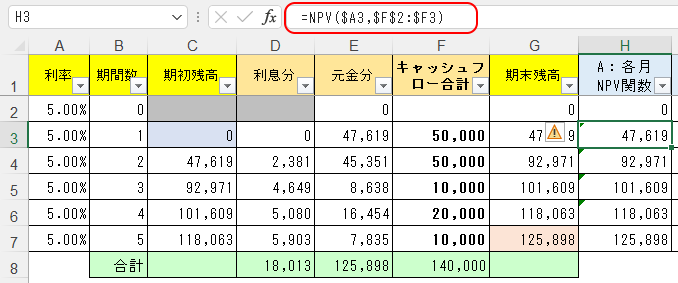
NPV関数の構成は
=NPV(割引率 , 値1,値2,・・・・・・値254まで)
というものだが、値1~値254というのは、あまり気にしなくて良いかと。通常は、連続したセル範囲を1回指定すれば良いだろう。
そして上記の例「=NPV( $A3 , $F$2:$F3 )」という式では、F2セルというのは何も値が入っていなくて、いわばその余分なセルまで参照範囲に入っているけど、これは問題ない。
NPV関数は、キャッシュフローが生じているセル範囲さえ指定できていれば、他に空欄のセルなどが範囲に加わる分には問題ないということだ。
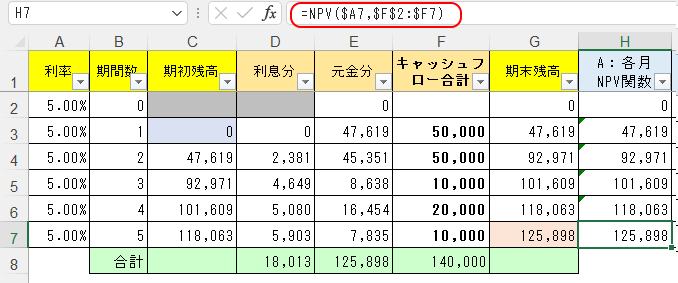
また説明のために、H3セル~H7セルまでNPV関数を埋めたけど、最終的に求めたい答えの125,898円というのは、H7セルに入れた式
=NPV($A7,$F$2:$F7)
で一発で求められる。
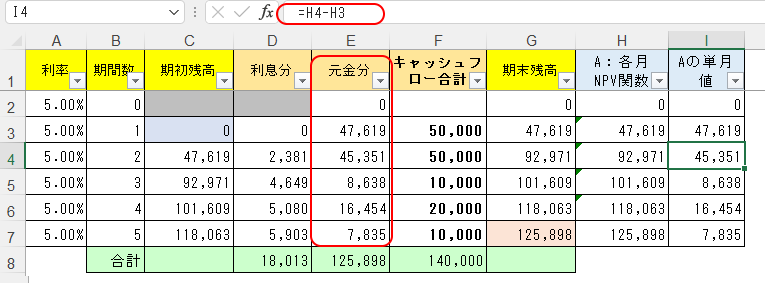
また、H列に求めたNPV関数の結果について、各月の単月値を求めたのがI列になるけど、これがE列(通常の数式で求めた現在価値)と合致することを確認しておく。
初期投資を加味して考える
初期投資が回収できるのか
さて、NPV関数の本当の使い道はここからで、初期投資を回収できるかということを考えてみる。
先ほど保留しておいた第0期に、130,000円の投資をした例を考えてみる。
これは支出をするキャッシュフローなので、マイナス値でF2セルに-130,000と記入する。
F列で発生するプラスのキャッシュフローは140,000円なので、最終的な収支もプラスになりそうだが、どうもG7セルの結果-4,102円だけ足りなくなるようだ。割引率5%のせいのようで。
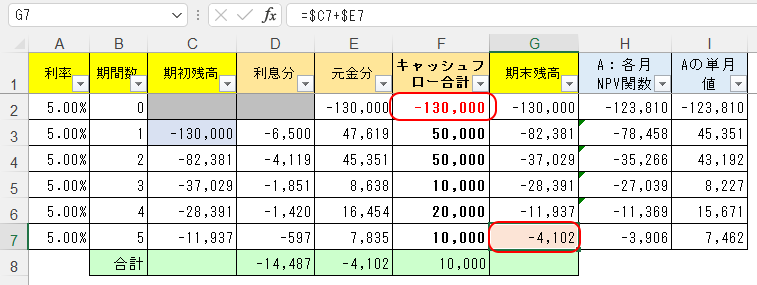
つまりここから分かるのは、<割引率5%のもと・5期で初期投資を回収しようと思った場合、初期投資130,000円では収支が合わない>という投資判断だ。
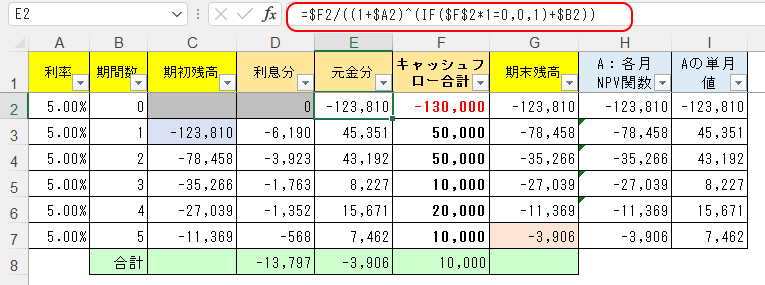
ちょっと上図では、I列とE列の数値が合わなくなってるけど、それは第0期が加わったからで、ちょっとE列の計算式を変えておこう。
E2セルに「 =$F2/((1+$A2)^(IF($F$2*1=0,0,1)+$B2)) 」と入れて、後はそれを縦にコピーすれば良い。
初期投資金額を変えてみる
じゃあ先ほど、初期投資を加味しないケースで答えが125,898円と求められたので、(小数点以下の数字があるけどそれは無視してみて)、F2セルに-125,898と入れてみよう。
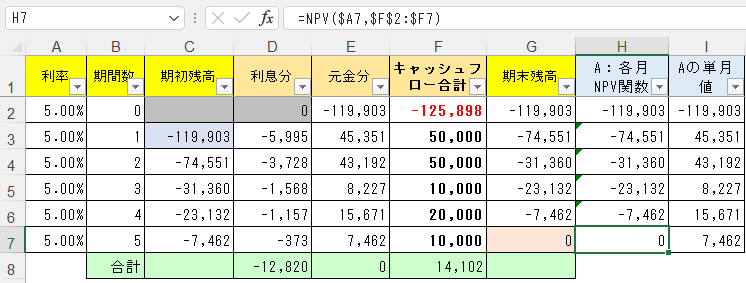
すると予想通り、最終的な残高(G7セル、H7セル)は0になる。
つまり125,898円以下の初期投資額ならば、F3セル以降の獲得キャッシュフロー合計140,000円をもって収支が合うということになる。
IRR関数:割引率を変えてみる
じゃあ今のは初期投資額を130,000円→125,898円に変えてみたけど、割引率5%というのが変われば130,000円が適切な投資額になることもあるはずだ。
その割引率、つまりNPV関数の結果が0になる割引率を求める関数がIRR関数だ。
定期的なキャッシュフローに対する内部利益率を求める、などと一般には説明される。
IRR関数の引数構成は
=IRR(範囲, [推定値])
で、[推定値]は通常省略して良いだろう(省略すると推定10%とみなされる)。
また「範囲」には、負の数(投資や支払い)と正の数(収益)がそれぞれ1つ以上含まれている必要がある。
では複合参照にしっかり気を付けて、J7セルに
=IRR($F$2:$F7)
と入れて、それをJ3セルまで貼り付ける。J2セルは、初期投資した第0期であり、ここで投資回収できるわけがないので空欄にしておく。
すると下図のように、初期投資125,898円のもとでは、第5期にちょうど投資回収できる割引率は5%だ。
そして割引率1.62%だったら、第5期を待たず第4期のうちに投資回収できるし、割引率-7.84%なら第3期で投資回収できることになる。
ただ、割引率がマイナス値というのは実務上「あり得ない」に近い(将来価値=今すぐ使えない価値 が現在価値より大きいということになり、通常考えられない)。
だから、-7.84%とかいうマイナス値の割引率は、計算上でやむなく求められてしまったというだけで、これを実務上の答えとして適用しようと思わない方が良いだろう。

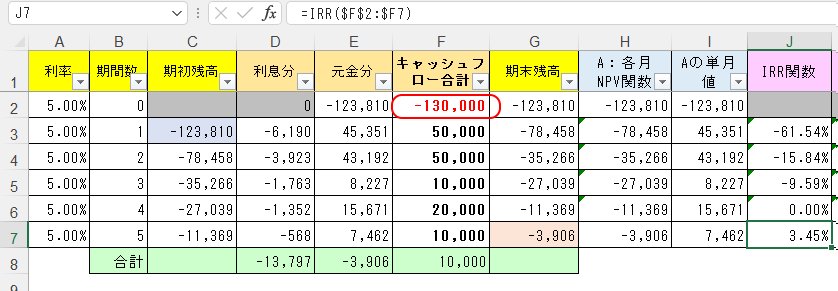
ではF2セルの初期投資を-130,000円に書き換えてみると、J7セルに求められた割引率は3.45%になる。
割引率3.45%のもとでなら、初期投資130,000円は5年でちょうど回収できるということだ。
また第4期についてIRR関数の結果は0%になってるけど、F3:F6に示す第4期までの合計キャッシュフローがちょうど130,000円なので、然もありなんということだ。
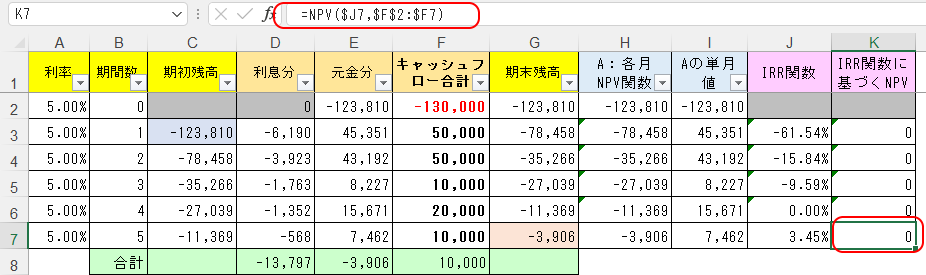
IRR関数は、NPV関数の結果が0になる割引率を求める関数だと説明したが、下図のK列でNPV関数を実際に入れて検証している。
またIRR関数でJ列に求めたそれぞれの割引率を、A列に値のみ貼り付けして検証してみるのも良いだろう。
たとえば第3期・J5セルの-9.59%をA2:A7セルに値のみ貼り付けすれば、G列=期末残高が第3期で0になる。
今回扱ったNPV関数は、①一定の期間で、②一定ではないキャッシュフロー金額 に対して現在価値を求めるものだ。
次回の記事では、①の期間すら一定ではないケースを処理する、XNPV関数を取り上げる。
スポンサーリンク