スポンサーリンク
前回の記事で、Excel財務関数の中でも、終価係数・年金終価係数という係数に関わるFV関数をメインに扱った。
それで将来価値というのを求められるわけだが、今回は将来価値の逆、現在価値を求めるPV関数をメインに取り上げる。
サンプルデータはこちら。
現価係数
前回の記事で、終価係数というやつをFV関数で求めるのに出した例題が、次のものだ。
→答え:1,218,994円
それではこれ、答えに出した1,218,994円の方を目標額として、それを貯めるには幾らの元手を用意すれば良いんですかってこともあるはずだ。
(もちろん実際はキリが良い1,219,000円とかいう目標額にするだろうが)問題文にすると、次のようになるだろう。
で、その場合の答えは100万円だけど、それを求める係数が現価係数であり、ExcelのPV関数で求められる。
終価係数の逆を取る
じゃあ終価係数について、計算する公式を思い出してみる。
元手a、利率r、期間nとして複利で運用したときの将来価値というやつは、終価係数というもので求めるけど、その式は
終価係数FV=a(1+r)n
だった。ならもう現価係数は、この逆を取れば良いだけだ。
上記で言うFVで求められる金額を今度は目標額とするので、それをSとすると、現価係数を求める式は
現価係数PV = S / (1+r)n
で良い。
その式で上記の問題の答えを求めたのが下図だ。前回記事で終価係数を求めるのに使った表の続きね。

次に、PV関数を使って求めたのが下図。まあここまでは終価係数と同様に簡単だ。

年金現価係数 : 最難関
じゃあ次に、年金現価係数というやつを扱う。これが最難関だろう。サンプルデータはこちら。
これまで扱ってきた終価係数とかのやつは、0円の状態から始まってそこにお金を足していき積み上げるものだった。
年金現価係数を考える場合は、最初に借金が500万円とかある状態から始まって、そこからお金を支払って減らしていき最終的に0円にするのをイメージすると良いかと思う。リース契約とかね。
問題文からして難しい
では問題文。
さて、こんな問題文で実際の試験にも出されるようなんだけど、予備知識もない状態でこの問題文を正しく読めるものだろうか。ちょっと説明不足じゃないかとも思うが。
返済予定表とかのイメージ図を出してくれれば良いけど、この文章じゃ解読するだけで凄く苦労するんじゃないだろうか。
可能かどうかと相談するものなの?
50,000×(5×12ヶ月)で300万円じゃないの?利息5%ってのがどう絡むの?
・・・というような疑問ばかりで、先に進めなくなっても当然だと思う。
リース契約や借入金の返済予定表の実物を見たことがある人ならともかく、それが無い人にはかなり厳しいんじゃないだろうか。
ではなんとか、私にできる限り、順を追って噛み砕いて説明していこうかと思う。
返済は元本とローンに分かれる
今回の問題文で「毎月50,000円ずつ返済する」とあって、これだけ見ると、305万円あったローンが翌月には300万円になるように思ってしまうんじゃないだろうか。
問題文にももう少し説明を書いてくれても良いと思うが、この「毎月50,000円ずつ」のうち、305万円あったローンから減ってくれるのは50,000円じゃない。利息分を引いて、もうちょっと少なくなった金額だけだ。
下図のように、まず1ヶ月目は、利息を11,040円取られ、50,000円からそれを差し引いた38,960円が元のローン残高から減る。
2ヶ月目は、利息を10,877円取られ、50,000円からそれを差し引いた39,123円が元のローン残高から減る。
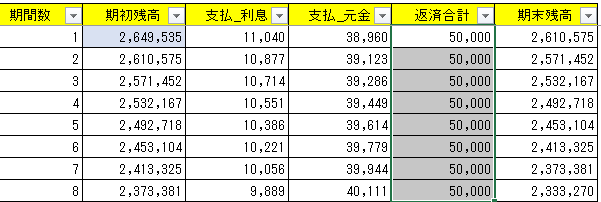
「毎月50,000円ずつ返済する」という文面が悪いと思うのだが、利息と元本を合わせて50,000円ずつ払わされるということであって、ローンの残高を減らしてくれるという意味の返済はもっと少なくなってしまう。
こういうのを「元利均等返済方式」といって、元本・利息に分かれた返済額のうち元本の方に該当する返済額は、期間経過に従って増えていく。
これに対し元本の方に該当する返済額を毎回50,000円とか固定させて、利息の方の返済額を期間経過に従って変化させて(減少させて)いく方式もあって、そちらは「元金均等返済方式」という。
毎回の返済額が一定なので計画が立てやすいというメリットにより、元利均等返済の方が主流らしいけどね。
計算式の導出

では、今回求めたい「借入可能額」とやらいうものは、図で青色で示してる2,649,535円が答えになるのだが、もちろんこれは最初は分からないので、この答えをxと置こう。
まず1ヶ月目は、このx円に対し年利5%の利息が取られる。でも支払は年単位じゃなく毎月させられるから、毎月の利率は<5%÷12>になる。
面倒だからこの<5%÷12>をrとしよう。
すると、1ヶ月目はx円に対しrを乗じた金額=rxが利息として取られる。
じゃあローンの元本そのものから減らされてくれる、元本返済額の方は<50,000 – rx>円だ。
で、1ヶ月目の返済をした後のローン残高をA1とすると、A1 = x – <50,000 – rx> = (1+r)x – 50,000円だ。
あまり変数を増やしたくはないけど、最後にR = 1+rとしよう。
すると、A1 = Rx – 50,000 となる。これが1ヶ月目の末残であり、2ヶ月目の月初残だ。
すると2ヶ月目は、A1に対しrを乗じたものが利息で、元本返済額は<50,000 – r・A1>だ。で、2ヶ月目の残高A2は、A1から元本返済額を引くことになるので、
A2
= A1 – < 50,000 – r・A1 >
= ( 1 + r )A1 – 50,000
1+r = R、A1 = Rx – 50,000 だったから、
A2
=R( Rx – 50,000 ) – 50,000
= R2x – 50,000R – 50,000
じゃあ次、3ヶ月目の残高A3 まで行ってみよう。A2のときと同様に計算して
A3
=RA2 – 50,000
=R( R2x – 50,000R – 50,000 ) – 50,000
=R3x – 50,000R2 – 50,000R -50,000
この調子で行くと、nヶ月目の月末残高Anは
An
= Rnx – 50,000Rn-1 – 50,000Rn-2 – ・・・ – 50,000R – 50,000
= Rnx – 50,000( 1 + R + ・・・ + Rn-1 )
= Rnx – 50,000× ( Rn-1) / (R – 1)
R = 1 + r だったから、
Rnx – 50,000× ( Rn-1) / (R – 1) = (1 + r)nx – 50,000{ ( 1 + r )n-1 } / r
さて今回は、もともと何百万円かあったリースを、60ヶ月かけて返済し最終的にゼロにするのだった。
つまり、60ヶ月目の月末残高A60がゼロにならないといけない。だから
A60 = 0
↓
( 1 + r )60x – 50,000× { ( 1 + r ) 60-1 ) / r = 0
↓
( 1 + r )60x = 50,000× { ( 1 + r ) 60-1 ) / r
↓
x = 50,000× { ( 1 + r ) 60 – 1 ) } / { r ( 1 + r )60 }
ではこれを一般化して、毎回の利率r、支払回数n、毎回の返済額tとすると、
年金現価係数による現在価値PV = t { (1 + r )n -1 } / { r( 1 + r )n }
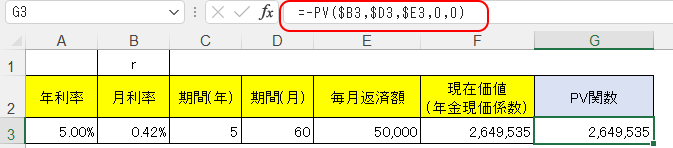
となる。これを使って、年金現価係数による現在価値を求めたのが下図。

で、PV関数で同じものを求めたのが下図。
資本回収係数 → ここでもPMT関数
それでは、年金現価係数の問題を再掲。
→答え2,649,535円
ではまた、これの逆を考えてみる。
答えとして2,649,535円が求められたわけだが、今度はその2,649,535円が最初にローン会社から提示されたとしよう。
それに対して毎回の返済額は幾らになるか(答え:50,000円)、シミュレーションしないといけないというものだ。
それを求める係数が、資本回収係数というものだ。
問題文としては、こんな感じか。
→答え:50,000円
これも、「毎月の返済額」という言葉は、<元本+利息>の返済額だと明記してほしいと思えるけどね。
じゃあ、年金現価係数による現在価値PVの計算式を再掲。
年金現価係数による現在価値PV = t { (1 + r )n -1 } / { r( 1 + r )n }
で、今回はこの式におけるtを求めたいわけ。これが毎回の支払額だからね。
では、左辺のPVは今回は所与の値とされるわけで、これをSとおこう。
求めるtの値つまり資本回収係数による毎回返済額は、逆数を取れば良いだけなので次の通りになる。
資本回収係数による毎回返済額PMT= Sr( 1 + r )n / { (1 + r )n -1 }
となる。これを使って、資本回収係数による毎回返済額を求めたのが下図。

じゃあこれを求めるExcelの関数は、PMT関数だ。
前回の記事で、減債基金係数というのを求めるのにもPMT関数が登場したんだが、その時は年金終価係数に対応する毎回の積立額を求めるのに使った。
そして今回は、年金現価係数に対応する毎回の返済額を求めるわけで、そういう毎回の積立・返済額を求めるのにPMT関数は使えるというわけだ。
そのPMT関数で、実際に毎回の積立額を求めたのが下図。

関数の構成
PV関数の構成
ではまず、今回のPV関数の構成について。
まず、現価係数を求めたときのPV関数。
=-PV( $B3, $D3, $E3, 0 , 0)

次に、年金現価係数を求めたときのPV関数。
=-PMT( $B3, $D3, $G3,0 , 0)

PV関数の引数の構成を改めてまとめ直すと、次のようになるということだ。③定期支払額と④現在価値について、現価係数を求める場合と年金現価係数を求める場合とでひっくり返る。
| ①利率(必須) | 年利率が与えられているが月単位で計算する場合は、12で割る。 |
| ②期間(必須) | 返済や積立の期間。 年単位で期間が与えられているが月単位で計算する場合は、12を乗じる。 |
| ③定期支払額(必須) |
毎回支払う金額。 現価係数を求める場合は、空欄か0 (現価係数って、1回入金してそれきりだから、定期支払は無い) |
| ④将来価値 (省略可) |
将来受け取る残高。積立貯蓄の場合は、満期受取額を指定する。以下、リースなど借入金を完済する場合を想定すると、 現価係数を求める場合は、元手の金額を書く |
| ⑤支払期日 (省略可) |
0(省略)→月末・期末の支払 今回の解説では、月末支払=0 を想定して進める。 |
PMT関数の構成:資本回収係数と減債基金係数
では次に、資本回収係数を求めたPMT関数の構成。
PMT関数って、前回の記事で扱った際には減債基金係数というのを求めた。
まとめると、FV関数・PV関数・PMT関数はそれぞれ次のような2つずつの係数を求められる。
ただもうこれは言葉で覚えるとかじゃなくて、状況次第で引数にはこれしか当てはめられないな・こう使うんだなという感覚を身に付けていくことになるだろう。
| FV | 終価係数 |
| 年金終価係数 | |
| PV | 現価係数 |
| 年金現価係数 | |
| PMT | 資本回収係数 |
| 減債基金係数 |
そしてPMT関数について、資本回収係数・減債基金係数それぞれに対する使い分け方を混じえて書いてみる。
| ①利率(必須) | 年利率が与えられているが月単位で計算する場合は、12で割る。 |
| ②期間(必須) | 返済や積立の期間。 年単位で期間が与えられているが月単位で計算する場合は、12を乗じる。 |
| ③現在価値(必須) |
将来価値が与えられてて、そこから毎回の積立額などを求める場合に記入。 |
| ④将来価値 (省略可) |
現在価値が与えられてて、そこから毎回の積立額などを求める場合に記入 |
| ⑤支払期日 (省略可) |
0(省略)→月末・期末の支払 今回の解説では、月末支払=0 を想定して進める。 |
実際に返済予定表を作る
さて今回も、上記の長々とした説明は、小賢しい数式をこねくり回しただけだ。
やはり実際に、自分で5年分とかの返済予定表を作ってみないと、本当に分かることはできないだろう。
今回は、やはり年金現価係数に関する下記の問題が最難関なので、これについて予定表を作ってみよう。
サンプルデータはこちら。
→答え2,649,535円
上記の問題に対する表の作り方は、下図のような感じでやると良いだろう。
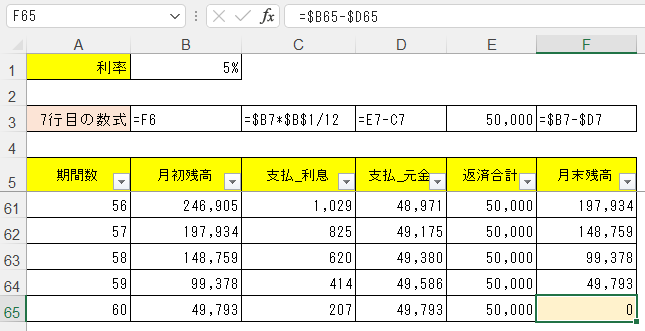
最終的な答え2,649,535円はB6セルに書き込むわけだけど、7行目の各セルに入れる数式は、下図の3行目「7行目の数式」に示した通り入れれば良い。
そしてその数式を、8行目以降にもコピーしていく。
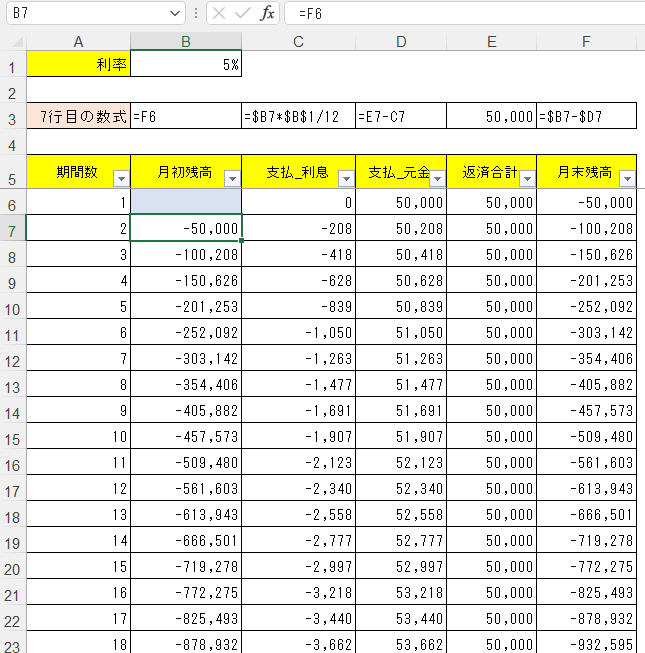
そしてB6セルに入れる答えは、PV関数で次のように求められる。
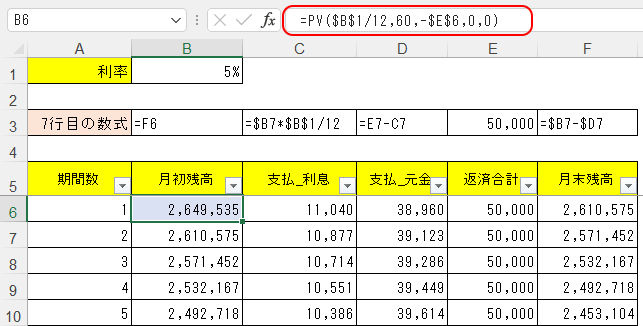
そしてこのPV関数が本当に正しいのかは、最後の60ヶ月目において「月末残高」が0円になって終わっていることで確認しよう。
ついでに 元金・利息の返済額を求める財務関数
余談だが、C列の利息については、<月初残高×1ヶ月あたり利率>で求めてたけど、これを求めるためのIPMTという関数もあって、次のように式を入れると良い。
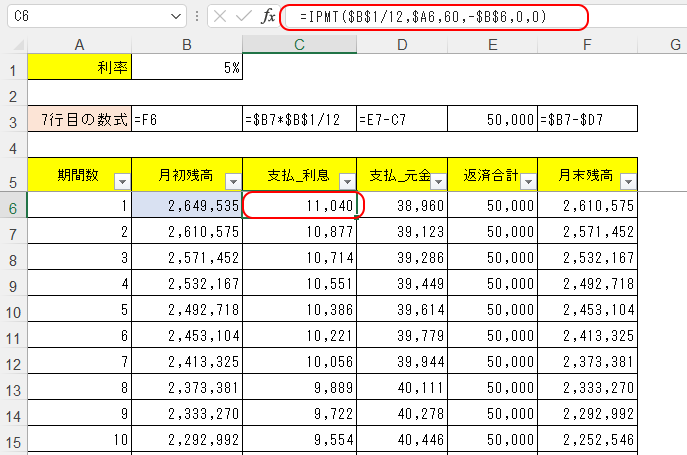
そして、D列の元本部分返済額については、これを求めるための財務関数としてPPMT関数がある。
式の入れ方は次の通りだ。
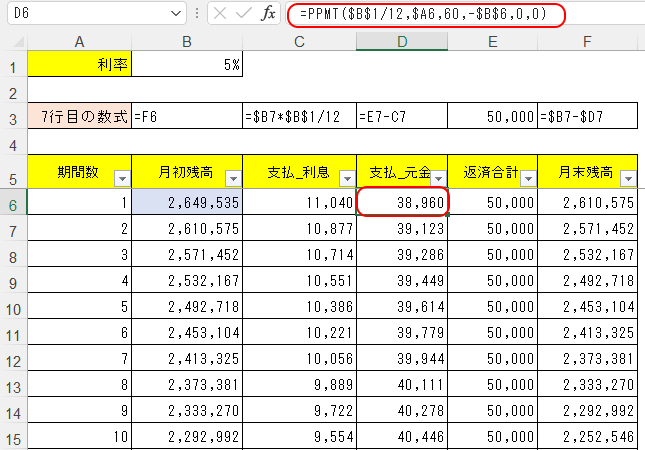
そして、
資本回収係数による毎回返済額PMT = PPMT + IPMT
という関係性になっている。
もうこんなのくらいなら普通に、財務関数じゃない数式で求めるほうが、安心だろうけどね。
利率を求める関数もある
最初に決めた現在価値(リース料総額)と毎回返済額の情報から、利率を求めるRATE関数っていう関数もある。
この利率を求めるのは、もう数学的に数式を定義するのは不可能なはず。
年金現価係数のときの数式を見直してもらうと分かるが、rについて解ききれる方程式にはなってないからだ。
式の入れ方は次の通りだ。推定値っていうのは、省略すると利率10%という推定値を指定したとみなされる。
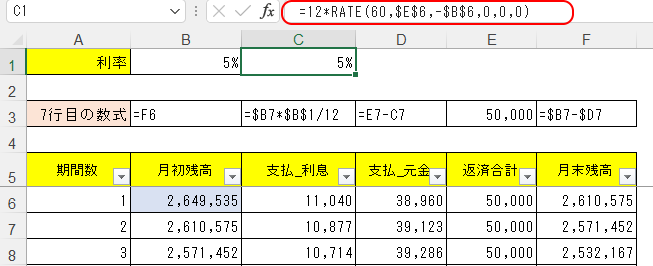
6つの係数とExcel財務関数 まとめ
それではここまで扱ってきた、「6つの係数」とExcel財務関数について、改めてまとめてみる。
| 係数 | Excelの関数 | 内容 |
| 終価係数 | FV | 最初に1回こっきり入金したお金が、定期的に利息が付く複利のもとで、将来いくらに増えるか。 |
| 年金終価係数 | 終価係数とは違い、入金は1回こっきりではなく定期積立する条件で、それら各期の積立に利息が付く複利のもとで、将来いくらに増えるか。 | |
| 減債基金係数 | PMT | 年金終価係数の問題で、「将来累計いくらに増やしたい」という目標が先にあったときに、それに対応する毎期の積立金額はいくらにすれば良いか。 |
| 現価係数 | PV | 終価係数の逆。将来最終的に得たい累積の目標額を決めて、それに対して最初に1回こっきり入金するお金の額を求める。 |
| 年金現価係数 | ローンの返済が典型。<利息+元本>の額を毎月均等に返済していく元利均等返済において、その返済させられる額から、借入金額を求める。 | |
| 資本回収係数 | PMT | 年金現価係数の問題で、リース料総額といった目標額が先にあったときに、それに対応する毎期の積立・返済金額はいくらにすれば良いか。 |
スポンサーリンク