スポンサーリンク
今回から、Excelの財務関数というやつについて取り上げてみる。
私もそんなに使うことはない関数だし、Excelの学習項目で優先順位が高い項目とはいえないと思うけど、最近自分が勉強してることと関わったりしているので、書いてみることにした。
例題:将来価値―FV関数
将来価値
では例題。
毎月末に5,000円を積み立てる積立において
3年後の将来価値はいくらになるか?
将来価値なんて言われて、サラッと分かるだろうか。
ひとまずその将来価値ってやつを求めるのが、FV関数だ。FVはFuture Valueで、文字通り将来価値のことだ。
で、将来価値というのは、満期まで来たときの、ローンの残高や積立の満期受取額ということで解説されている。
だがそれも、言葉だけではイメージが持ちにくいだろうなと思う。やはり自分で作ってみないとね。
FV関数の構成
FV関数の構成は
となっている。それぞれ次の通りだ。
| ①利率(必須) | |
| ②期間(必須) | 返済や積立の期間。 |
| ③定期支払額(必須) | 毎回支払う金額。 計算結果は、手元に入る金額はプラス表示、手元から出ていく金額はマイナス表示というルール。 |
| ④現在価値 (省略可) |
頭金。 |
| ⑤支払期日 (省略可) |
0(省略)→月末・期末の支払 今回の解説では、月末支払=0 を想定して進める。 |
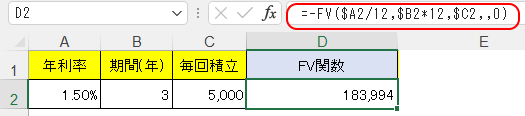
ExcelでA2セルに①利率、B2セルに②期間、C2セルに③定期支払額を入れておいて、FV関数を
と入れれば、上記の例題に対する答えが183,994円と得られる。
A2セル・B2セルには年単位を想定した数値を入れているので、A2セル=年利率は12で割り、B2セル=期間は12を乗じるということをしないといけない。これがまたややこしい。
財務関数の中身って?
・・・というところまでで、大体のテキスト・サイトの解説は終わっていると思う。
私が見た限りではそうだ。
では上図でFV関数の結果として183,994円という答えが出ているが、本当にこの数字は正しいのだろうか。
FVなんて専用関数を使わず一般的な計算で、これをどうやって検算すれば良いのだろうか。
恐らく皆さんがFV関数とか使うことになるのは、「以前から代々引き継いできたExcelフォーマットに関数が組み込まれてるから、引き続き使う」ということがほとんどだろう。私もそうだ。
そして、求め方を説明しろとか(数式を全く読もうともしない上司から)言われたら、
「いや、前からFV関数っていうのがExcelに入れてあって、それで答えが求まっちゃうんだから。説明しろったって、専門的すぎてわけ分からない関数なんだから。」
となる人も多いのではないだろうか。
まあ本当、1つの式で答えが出るようになっててブラックボックス化されているものだから、いきなり聞かれてソラで中身を答えろとか言われても、そうできるものでもないだろう。
そして、この説明を詳細にしてくれてるサイトもなかなか見付からないから、よほど特別に勉強してる人とかでないと検算も難しいだろう。
Excelの財務関数と「6つの係数」
そこで次回の記事から、財務系関数の中でも将来価値とか現在価値とかの金額に関する
- FV関数
- PV関数
- PMT関数
について、数学的な考えも混じえて中身を見ていきたいと思う。
そしてこれら関数は、FP(ファイナンシャル・プランナー)試験で扱う6つの係数
- 終価係数
- 現価係数
- 年金現価係数
- 年金終価係数
- 資本回収係数
- 減債基金係数
を求められる関数だ。
Excelの財務関数と、「6つの係数」の対応関係は次の通り。
関数に対する引数の入れ方によって、求める係数を分けられるようになっている。
| FV | 終価係数 |
| 年金終価係数 | |
| PV | 現価係数 |
| 年金現価係数 | |
| PMT | 資本回収係数 |
| 減債基金係数 |
ただそのFP試験でも、それら6つの係数については、0.091とかいろいろな係数の表が与えられて、ただその係数を掛け算したりするだけで問題は解けるようになっている、はずだ。
それら係数を求めるにはどんな数学的な計算をすれば良いのかとか、受験においては中身を深く突き詰める必要はないはずで、多くの受験生もそこまでやってないんじゃないだろうか。
今回私がやりたいのは、それら専用の係数や関数を使わずに一般的な数学の式だけでやろうとするとどうなるかってことだ。
というか、例題では3年=36ヶ月の例を取り上げたが、36ヶ月分のことを「FV関数を使うだけで求められました」「係数を掛け算すれば求められました」で済ませるべきではないだろう。
実際に、36ヶ月の予定表を作ってみるべきだ。次回からはそういった観点から進めていく。
スポンサーリンク