スポンサーリンク
前回の記事で、①一定の期間で、②一定ではないキャッシュフロー金額 に対して現在価値を求め投資判断などに用いるNPV関数を扱った。
今回は更に複雑な、①期間も一定ではない、②キャッシュフロー金額も一定ではない 条件下で現在価値を求め投資判断などに用いるXNPV関数を扱う。
XNPV関数:返済期日も返済金額も不規則
では前回の記事で扱った表を流用して、下図のような表を作成してみた。ファイルはこちら。
前回の流用なので、表の中身について細かい説明は少なめにしていく。
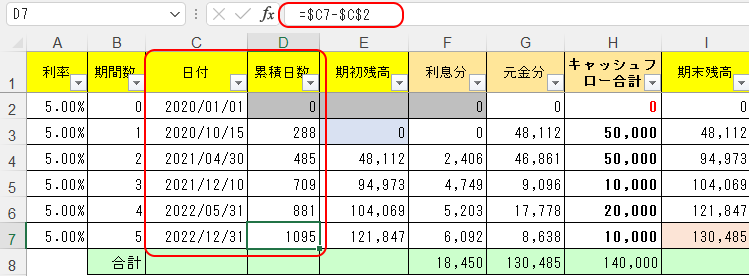
前回との違いはC列・D列で、キャッシュフローの発生する日付・期間が不規則だということだ。
H列のキャッシュフロー金額も不規則ね。
今回扱うXNPV関数は、不規則な期間に対応した計算をするので、どうしても期間を「日」単位に直しておかないといけない。それをやったのがD列だ。
前回と同様、H2セルの初期投資額は無しにしておくけど、XNPV関数はちょっとデリケートなので、ここを空欄にしてはおけない。
H2セルには、0円と明確に書いて埋めておく。
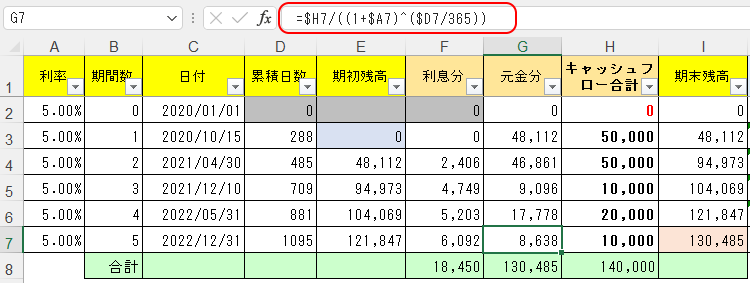
ではG列に求める各月の現在価値は、年単位の割引率5%(A列)を、365日で割って累積日数(D列)を乗じたものとして算出する。
G7セルの式は
=$H7/((1+$A7)^($D7/365))
というようになり、これをG2:G7セルまでコピーする。
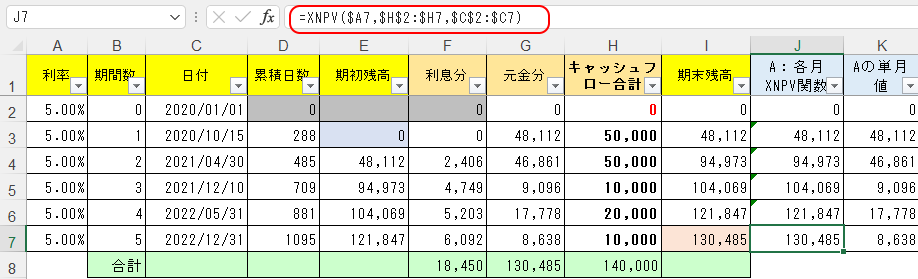
そしてこの結果として、I列の期末残高が求められる。そしてこれと合致する数値が、XNPV関数で求められる。
XNPV関数の構成は
=XNPV(割引率, 値, 日付)
というもの。
NPV関数とはちょっと勝手が違って、割引率にマイナス値を指定するとエラーになる(ヘルプに明記されてないけど)。
そしてJ7セルに
=XNPV($A7,$H$2:$H7,$C$2:$C7)
とXNPV関数を入れてJ2:J7セルまでコピーすれば、I列と合致する値がJ列に求められる。
またそれらの各月の差額をK列に取って、G列の現在価値と合致する値が求められる。
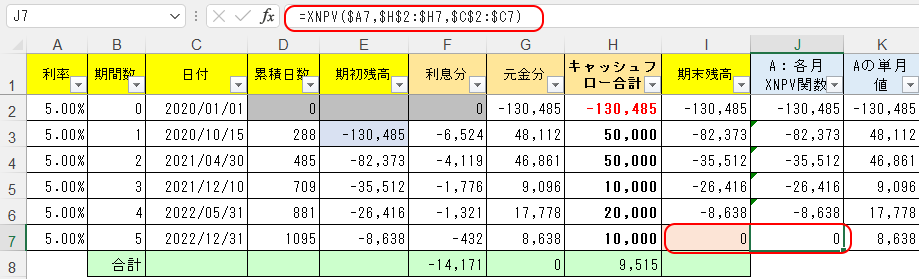
では上図でI7セルに、最終的な残高が130,485円と求められているが、これを初期投資額とすればジャストで回収しきれることになりそうだ。
下図の通りH2セルに、マイナス値で-130,485円と入力すれば、J7セルの最終残高が0になることが確認できる。
XIRR関数:割引率を変えてみる
では次に、初期投資額を-120,000円と変えてH2セルに入力して、それがちょうど回収できる割引率を求めてみよう。
つまり、XNPV関数の結果を0にする割引率を求めるわけで、それ用の関数がXIRR関数だ。
IRR関数と同様、定期的なキャッシュフローに対する内部利益率というものが求められる。
XIRR関数の構成は
=XIRR(範囲, 日付, 推定値)
というもの。
「範囲」には、負の数(投資や支払い)と正の数(収益)がそれぞれ1つ以上含まれている必要がある。
そしてL7セルに
=XIRR($H$2:$H7,$C$2:$C7)
とXIRR関数を入れ、それをL2:L7セルにコピーする。
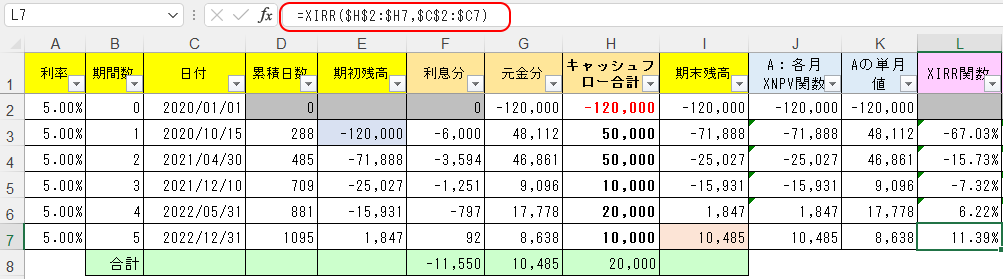
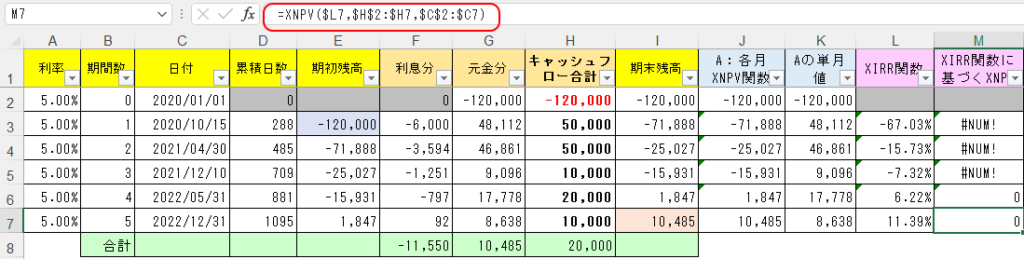
そのXIRR関数による割引率(L列)を適用した結果のXNPV関数を、M列に入れれば、結果が0になるのが確認できる。
ただし割引率がマイナス値の場合は、XNPV関数の結果はエラー値になってしまう。またこの場合は、初期投資に対する採算は取れないということだ。
現在価値の関数 まとめ
それでは現在価値を求める財務関数として、PV・NPV・XNPV関数を扱ったが、最後にそれらの違いについてまとめてみる。
| 現在価値の関数 | 期間 | キャッシュフロー金額 | 利子率(割引率)を 求める関数 |
| PV | 一定の規則に従う | RATE | |
| NPV | 一定の規則に従う | 不規則 | IRR |
| XNPV | 不規則 | XIRR | |
NPV・XNPV関数はPV関数より複雑な計算ができて、PV関数の上位互換にも見えるが、PV関数なら返済予定表を作り込まなくてもセル1個で答えを一気に求められる。
予定表が作られている状況なら、最初からNPV関数などを使えば良いというケースも多いだろう。それらは適宜判断するところだ。
スポンサーリンク